Konsep dan Contoh Soal Dinamika Rotasi - Fisika SMA Kelas 11

Dalam materi fisika SMA kelas 11, ada materi fisika tentang torsi, kesetimbangan benda tegar, dinamika rotasi, dan pusat massa. Pada materi fisika tersebut, model soal sangat bervariasi mulai dari yang sederhana sampai soal yang memiliki karakteristik model soal HOTS. Untuk membantu teman-teman, tim lakonfisika.net telah menyusun materi fisika tersebut beserta contoh soalnya. Langsung saja silakan bisa disimak penjelasan berikut ini.

1. Konsep Torsi atau Momen Gaya

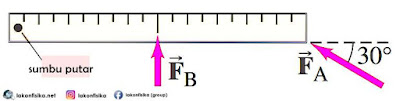
Untuk memahami konsep torsi atau momen gaya, ada 3 hal yang perlu diketahui oleh teman-teman, yaitu posisi sumbu putar, posisi dan arah gaya, serta lengan gaya. Pada benda yang bergerak rotasi (melingkar), pasti ada satu titik yang menjadi acuan atau pusat putarannya, itulah yang disebut sebagai sumbu putar. Sedangkan penyebab benda tersebut berotasi, adalah gaya yang bekerja pada posisi tertentu dari sumbu putarnya. Nah, jarak antara posisi bekerjanya suatu gaya dan sumbu putar itulah yang disebut sebagai lengan gaya. Untuk lebih jelasnya bisa dilihat dalam ilustrasi gambar.

Torsi adalah hasil perkalian dari gaya dan lengan gaya, dengan syarat keduanya harus saling tegak lurus. Artinya kalau keduanya belum saling tegak lurus, maka harus dicari komponen yang saling tegak lurus. Pada gambar di atas (dianggap sebagai batang tak bermassa sehingga tidak memiliki gaya berat), bekerja gaya ${{F}_{A}}$ pada titik yang berjarak ${{r}_{A}}$ dari sumbu putar dan gaya ${{F}_{B}}$ pada titik yang berjarak ${{r}_{B}}$.

Antara ${{F}_{B}}$ dan ${{r}_{B}}$ sudah saling tegak lurus, maka:

${{\tau }_{B}}={{F}_{B}}\cdot {{r}_{B}}$

Sedangkan antara ${{F}_{A}}$ dan ${{r}_{A}}$ belum saling tegak lurus, maka harus ditentukan komponen yang saling tegak lurus terlebih dulu. Caranya bisa dicari komponen uraian ${{r}_{A}}$ yang tegak lurus terhadap ${{F}_{A}}$ atau komponen uraian ${{F}_{A}}$ yang tegak lurus terhadap ${{r}_{A}}$. Sehingga nilai torsi oleh gaya ${{F}_{A}}$ adalah:

${{\tau }_{A}}={{r}_{Ay}}\cdot {{F}_{A}}$ atau ${{\tau }_{A}}={{r}_{A}}\cdot {{F}_{Ay}}$

Dengan nilai ${{r}_{Ay}}={{r}_{A}}\sin \alpha$ dan ${{F}_{Ay}}={{F}_{A}}\sin \alpha $, maka:

${{\tau }_{A}}=({{r}_{A}}\sin \alpha )\cdot {{F}_{A}}$ atau ${{\tau }_{A}}={{r}_{A}}\cdot ({{F}_{A}}\sin \alpha )$

Selanjutnya total torsi pada batang tersebut adalah:

\[\sum{\tau ={{\tau }_{A}}-{{\tau }_{B}}}\]

\[\sum{\tau =({{r}_{A}}\cdot {{F}_{A}}\sin \alpha )-({{r}_{B}}\cdot {{F}_{B}})}\]

(nilai ${{\tau }_{A}}$ positif karena kecenderungan rotasi searah jarum jam, sedangkan ${{\tau }_{B}}$ negatif karena kecenderungan rotasi berlawanan jarum jam)

Contoh Soal Torsi atau Momen Gaya

Dua buah gaya ${{F}_{A}}=30N$ dan ${{F}_{B}}=20N$ bekerja pada sebuah batang penggaris (massa diabaikan) yang dapat berputar terhadap sumbu di ujung sebelah kirinya (lihat gambar). Gaya ${{F}_{B}}$ bekerja secara tegak lurus tepat di tengah penggaris. Jika panjang penggaris adalah 50 cm, maka:
a. torsi manakah yang lebih besar? Ataukah keduanya sama?
b. berapakah torsi total yang bekerja pada penggaris tersebut?

Jawab:

a

${{\tau }_{A}}={{F}_{Ay}}\cdot {{r}_{A}}$

${{\tau }_{A}}={{F}_{A}}\sin {{30}^{o}}\cdot {{r}_{A}}$

${{\tau }_{A}}=30\cdot \frac{1}{2}\cdot 0,5=7,5N$

${{\tau }_{B}}={{F}_{B}}\cdot {{r}_{B}}$

${{\tau }_{B}}=20\cdot 0,25=5N$

Maka nilai ${{\tau }_{A}}>{{\tau }_{B}}$

b

$\sum{\tau ={{\tau }_{A}}+{{\tau }_{B}}}$

$\sum{\tau =7,5+5}=12,5N$

(dua torsi memiliki arah yang sama/berlawanan jarum jam, tanda negatif bisa diabaikan dan diganti positif karena tanda hanya kesepakatan untuk membedakan arah)

2. Kesetimbangan Rotasi Benda Tegar

Syarat utama dalam kesetimbangan rotasi adalah adanya kondisi kesetimbangan torsi ($\sum{\tau }=0$). Selanjutnya, kondisi kesetimbangan torsi itu juga bisa dikombinasikan dengan kesetimbangan gaya ($\sum{F}=0$). Untuk melakukan analisis torsi, caranya sama dengan contoh soal di atas, tetapi memang nanti juga menyesuaikan model soal. Nah, seperti yang sudah disampaikan, bahwa topik kesetimbangan benda tegar ini memiliki model soal yang variatif dari mudah sampai soal HOTS fisika.

Contoh Soal Kesetimbangan Benda Tegar

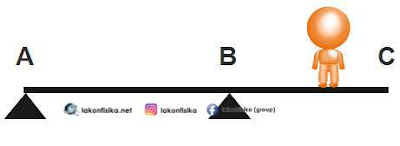
Papan AC bermassa 40 kg dan memiliki panjang 3 m. Jarak antara tumpuan A dan B adalah 2 m (di B papan dapat berputar). Sebuah robot (massa 25 kg) berjalan di atas papan dari A menuju ke C. Berapa jarak minimum robot itu dari titik C agar papan tetap setimbang (ujung papan A hampir terangkat ke atas)?

Jawab:

$\sum{\tau =0}$

${{\tau }_{r}}-{{\tau }_{b}}=0$

${{w}_{r}}\cdot {{r}_{r}}-{{w}_{b}}\cdot {{r}_{b}}=0$

${{w}_{r}}\cdot {{r}_{r}}={{w}_{b}}\cdot {{r}_{b}}$

$250\cdot {{r}_{r}}=400\cdot (2-1,5)$ 

(posisi w batang/papan tepat di tengah atau 1,5 m dari ujung A)

$250\cdot {{r}_{r}}=200$

${{r}_{r}}=0,8m$

Maka posisi robot dari titik C adalah $BC-{{r}_{r}}=1-0,8=0,2m$

3. Momen Inersia

Sebelum kita belajar tentang dinamika rotasi, maka perlu dipahami dulu konsep tentang momen inersia. Dalam pembahasan dinamika rotasi, torsi total yang bekerja dalam suatu sistem adalah $\sum{\tau =I\cdot \alpha }$ dengan $I$adalah momen inersia sistem dan $\alpha $ adalah percepatan sudut rotasi. Momen inersia bisa dikategorikan menjadi dua, momen inersia benda titik (partikel) dan momen inersia benda tegar (rigid body). 

Persamaan momen inersia benda titik (partikel) adalah:

$I=\sum{(m\cdot {{r}^{2}})}={{m}_{1}}\cdot {{r}_{1}}^{2}+{{m}_{2}}\cdot {{r}_{2}}^{2}+{{m}_{3}}\cdot {{r}_{3}}^{2}+...$

$m$ adalah massa masing-masing partikel dan $r$ adalah jarak masing-masing partikel dari sumbu putar.

Sedangkan momen inersia benda tegar atau benda pejal, dapat dilihat pada tabel momen inersia berikut ini.

Contoh Soal Momen Inersia Partikel

Dua buah benda yang berukuran kecil masing-masing bermassa 5 kg dan 7 kg terhubung dengan batang kecil yang massanya diabaikan. Hitunglah momen inersia sistem saat:

a. diputar terhadap sumbu tepat di tengah keduanya

b. diputar pada sumbu berjarak 0,5 m di kiri massa 5 kg (lihat gambar)

Jawab:

a.

$I=\sum{(m\cdot {{r}^{2}})}$

$I=5\cdot ({{2}^{2}})+7\cdot ({{2}^{2}})$ (masing-masing benda berjarak 2 m dari sumbu putar)

$I=20+28=48kg.{{m}^{2}}$

b.

$I=\sum{(m\cdot {{r}^{2}})}$

$I=5\cdot (0,{{5}^{2}})+7\cdot (4,{{5}^{2}})$ (massa 5 kg berjarak 0,5 m dari sumbu dan massa 7 kg berjarak 4,5 m)

$I=1,25+141,75=143kg.{{m}^{2}}$

4. Dinamika Rotasi

Seperti yang sudah disampaikan sebelumnya, bahwa dalam pembahasan dinamika rotasi, torsi total yang bekerja dalam suatu sistem adalah $\sum{\tau =I\cdot \alpha }$. Persamaan itu biasa disebut sebagai Hukum II Newton untuk gerak rotasi. Teknik analisis torsi sama dengan cara pada penjelasan torsi dan kesetimbangan benda tegar di atas. Yang berbeda adalah ada percepatan sudut sistemnya. Artinya dalam kondisi ini sistem tidak dalam keadaan setimbang. Jadi dalam analisis sistem yang bergerak rotasi nanti dimungkinkan adanya kombinasi dengan Hukum II Newton untuk gerak translasi. Agar lebih jelas, bisa kita simak penjelasan dalam contoh soal berikut ini.

Contoh Soal Katrol - Dinamika Rotasi 

Seutas tali yang digantungi beban m = 0,1 kg, dililitkan pada sebuah katrol yang berbentuk silinder pejal. Massa katrol adalah 0,8 kg dengan jari-jari 10 cm. Awalnya katrol dalam keadaan diam dan terus bergerak dengan percepatan tertentu. Besar percepatan sistem katrol tersebut adalah...

Jawab:

$\sum{\tau =I\cdot \alpha }$

$r\cdot T=\frac{1}{2}\cdot {{m}_{k}}\cdot {{r}^{2}}\cdot \frac{a}{r}$

$T=\frac{1}{2}\cdot {{m}_{k}}\cdot a.................(1)$

$\sum{F=m\cdot a}$

$w-T=m\cdot a.................(2)$

Substitusi persamaan 1 ke persamaan 2

$w-\frac{1}{2}{{m}_{k}}a=ma$

$w=ma+\frac{1}{2}{{m}_{k}}a$

$0,1.10=0,1.a+\frac{1}{2}.0,8.a$

$1=0,5a$

$a=2{}^{m}/{}_{{{s}^{2}}}$

Jika ingin mencari tegangan tali, maka tinggal dilakukan substitusi nilai $a=2{}^{m}/{}_{{{s}^{2}}}$ ke persamaan 1.

5. Pusat Massa atau Titik Berat

Untuk mempelajari cara menentukan pusat massa benda tunggal atau pusat massa benda gabungan, silakan teman-teman bisa menyimak artikel model soal pada posting sebelumnya. Silakan langsung meluncur ke artikel pembahasan soal pusat massa.

Video Penjelasan Materi Dinamika Rotasi Kelas 11

Share this post