Konsep dan Contoh Soal Listrik Dinamis – Rangkaian Resistor - Fisika SMA Kelas 12

Materi Listrik dinamis akan banyak bercerita tentang muatan listrik yang mengalir lewat area tertentu di dalam ruang (secara khusus, ruang yang dimaksud adalah konduktor). Arus listrik digunakan sebagai istilah untuk menyatakan besar laju aliran muatan listrik tersebut. Pada materi fisika SMA kelas 12, beberapa topik yang termasuk bahan kajian listrik dinamis adalah:
a. hubungan arus listrik, hambatan atau resistansi, dan beda potensial yang dinyatakan dalam hukum Ohm
b. rangkaian resistor, yang terdiri dari rangkaian seri, rangkaian paralel, dan rangkaian campuran
c. hukum Kirchoff I tentang arus listrik dan hukum Kirchoff II tentang beda potensial. Khusus untuk topik ini, akan dibahas tersendiri pada artikel Konsep Hukum Kirchoff.

1. Konsep Arus Listrik

Aliran muatan listrik dalam suatu konduktor bergantung pada jenis material dan beda potensial pada konduktor tersebut. Arus listrik dalam konduktor dapat dianalogikan dengan aliran air dalam suatu pipa. Aliran air dalam pipa dapat diukur dengan menentukan jumlah air yang keluar dari kran dalam selang waktu tertentu (biasanya liter per menit).

Ilustrasi Aliran Muatan Listrik (Arus Listrik)

Untuk menentukan besar arus listrik, kita bisa memisalkan muatan bergerak dalam arah tegak lurus melewati luas penampang konduktor. Pada gambar di atas, $A$ merupakan ilustrasi luas penampang melintang suatu konduktor. Ada sejumlah muatan positif $\Delta Q$ yang melewati luas penampang $A$ dengan arah tegak lurus selama selang waktu $\Delta t$. Arus listrik didefinisikan sebagai laju aliran muatan listrik melintasi penampang tersebut. Sehingga besar arus listrik dapat dihitung dengan persamaan 1 di bawah ini.

${{I}_{rerata}}=\frac{\Delta Q}{\Delta t}\quad \text{dan }\quad {{I}_{sesaat}}=\frac{dQ}{dt}\quad \ldots \ldots \ldots \ldots \ldots \left( 1 \right)$

Ilustrasi Kecepatan Rata-Rata Aliran Muatan Listrik

Untuk menentukan kecepatan rata-rata aliran tiap muatan, kita asumsikan muatan listrik mengalir dalam konduktor berbentuk silinder dengan penampang melintang seluas $A$, seperti gambar di atas. Selanjutnya diambil potongan (segmen) sepanjang $\Delta x$ di antara dua luasan $A$, sehingga membentuk volume potongan sebesar $\Delta V=A\ \Delta x$. Jika dalam segmen volume tersebut ada sebanyak $n$ partikel muatan yang bergerak, maka jumlah total muatan adalah:


$\begin{align} & \Delta Q=n\,\left( \Delta V \right)q \\ & \Delta Q=n\left( A\,\Delta x \right)q \\ \end{align}$

Sehingga, untuk menentukan kecepatan rata-rata aliran muatan listrik $\left( {{v}_{d}} \right)$ dapat digunakan persamaan 2 berikut ini.


$\begin{align} & {{I}_{rerata}}=\frac{\Delta Q}{\Delta t} \\ & {{I}_{rerata}}=\frac{n\ A\ \Delta x\ q}{\Delta t} \\ & {{I}_{rerata}}=n\ A\ {{v}_{d}}\ q\text{ (nilai }\frac{\Delta x}{\Delta t}={{v}_{d}}\text{)} \\ & {{v}_{d}}=\frac{{{I}_{rerata}}}{n\ A\ q}\quad \ldots \ldots \ldots \ldots \ldots \left( 2 \right) \\ \end{align}$

2. Konsep Hukum Ohm

Untuk menghasilkan arus listrik dalam suatu rangkaian, dibutuhkan beda potensial antara dua ujung rangkaian tersebut. Berdasarkan eksperimen yang dilakukan oleh Georg Simon Ohm, besar arus listrik sebanding dengan beda potensial listrik $\left( I\propto V \right)$. Selain dipengaruhi oleh beda potensial listrik, Ohm menyatakan bahwa besar arus listrik juga dipengaruhi oleh resistansi atau hambatan $\left( R \right)$.  Hambatan merupakan perbandingan linier antara beda potensial dan kuat arus listrik. Hubungan antara beda potensial $\left( V \right)$, kuat arus listrik $\left( I \right)$, dan hambatan $\left( R \right)$ dinyatakan dalam Hukum Ohm dengan persamaan 3 berikut ini.

$V=I\ R\quad \ldots \ldots \ldots \ldots \ldots \left( 3 \right)$

Bahan konduktor yang merupakan penghantar listrik, ternyata juga memiliki nilai hambatan $\left( R \right)$. Nilai hambatan konduktor dipengaruhi oleh konstanta resistivitas bahan $\left( \rho  \right)$. Dalam suatu kawat konduktor, nilai hambatan berbanding lurus dengan resistivitas bahan dan panjang konduktor $\left( l \right)$, serta berbanding terbalik dengan luas penampang melintangnya $\left( A \right)$. Nilai hambatan pada kawat konduktor dapat ditentukan sesuai hubungan persamaan 4 berikut ini.

$R=\rho \,\,\frac{l}{A}\quad \ldots \ldots \ldots \ldots \ldots \left( 4 \right)$ 

Berdasarkan sifat logam yang dapat berubah panjang (memuai atau menyusut) akibat perubahan suhu, nilai hambatan konduktor juga akan terpengaruh akibat perubahan suhu. Sesuai dengan persamaan 4, dapat dinyatakan bahwa $\rho \propto l$, artinya jika terjadi perubahan panjang, maka akan terjadi perubahan nilai hambatan pula. Besar nilai perubahan hambatan pada konduktor dengan koefisien muai $\alpha $ akibat terjadi perubahan suhu $\Delta T$ adalah:

$\Delta R={{R}_{o}}\ \alpha \ \Delta T\quad \ldots \ldots \ldots \ldots \ldots \left( 5 \right)$

Contoh Soal Hukum Ohm dan Hambatan Konduktor

Seorang teknisi ingin menghubungkan speaker dengan amplifier menggunakan kabel sepanjang 20 m. Kabel terbuat dari bahan tembaga dengan $\rho =1,68\times {{10}^{-8}}\Omega \cdot m$. Agar kualitas audio tetap baik, setiap kabel harus memiliki hambatan $0,1\ \Omega $. Tentukan:

a. diameter kawat yang digunakan

b. besar beda potensial atau drop voltage antara ujung-ujung setiap kabel tersebut, jika kuat arus pada tiap kabel adalah 4 A.

Jawab:

$\begin{align} & A=\rho \frac{l}{R} \\ & A=1,68\times {{10}^{-8}}\frac{20}{0,1} \\ & A=3,4\times {{10}^{-6}}\ {{m}^{2}} \\ \end{align}$

Dengan asumsi penampang berbentuk lingkaran, maka $A=\frac{1}{4}\pi {{d}^{2}}$.

$\begin{align} & d=\sqrt{\frac{4A}{\pi }} \\ & d=\sqrt{\frac{4\cdot 3,4\times {{10}^{-6}}}{3,14}} \\ & d\approx 2,08\times {{10}^{-3}}\ m\approx 2,08\ mm \\ \end{align}$

Nilai beda potensial atau drop voltage adalah:

$\begin{align} & V=I\,R \\ & V=4\cdot 0,1 \\ & V=0,4\ volt \\ \end{align}$

3. Energi Listrik dan Daya

Setiap detik aktivitas kita sekarang ini hampir tidak lepas dari penggunaan energi listrik. Pastinya, bentuk energi listrik perlu diubah menjadi bentuk energi lain sebelum digunakan, misalnya kipas angin, pemanas air, kulkas, handphone, dan peralatan lainnya. Dengan memahami konsep energi listrik, maka kita dapat menghitung estimasi penggunaan energi listrik setiap harinya. Setiap perlatan listrik, selalu mencantumkan jumlah konsumsi energi listrik setiap detiknya atau disebut sebagai daya listrik (electric power). Nilai daya listrik $\left( P \right)$berhubungan dengan beda potensial $\left( V \right)$, kuat arus listrik $\left( I \right)$, dan hambatan $\left( R \right)$. Hubungan besaran-besaran tersebut dapat ditentukan dengan persamaan berikut ini:

$P=V\ I\quad \text{karena nilai }V=I\ R\text{, maka: }\quad P={{I}^{2}}R\quad \text{atau }\quad P=\frac{{{V}^{2}}}{R}$ 

Sedangkan nilai energi listrik adalah $E=P\cdot t$.

Contoh Soal Energi Listrik dan Daya

Sebuah pemanas listrik mengalirkan arus sebesar 15 A dengan tegangan 120 V. Jika dalam sehari, pemanas tersebut digunakan selama 3 jam dan tarif listrik adalah Rp. 200,- per kWh, maka total biaya yang dihabiskan selama sebulan (30 hari) adalah...

Jawab:

Kebutuhan energi selama sebulan adalah:

$\begin{align} & E=P\cdot t \\ & E=\left( V\ I \right)\cdot \left( 3\ jam\ \times 30\ hari \right) \\ & E=\left( 120\cdot 15 \right)\cdot 90 \\ & E=162000\ Wh=162\ kWh \\ \end{align}$

Biaya listrik sebulan adalah $162\times \left( Rp.\ 200 \right)=Rp.\ 32.400$

4. Rangkaian Resistor (Rangkaian Seri Paralel)

Ilustrasi Rangkaian Resistor Seri dan Paralel

Pada suatu rangkaian elektronika, pasti tidak hanya ada satu buah resistor atau hambatan, tetapi ada beberapa susunan resistor. Susunan atau rangkaian dasar resistor terdiri dari dua jenis, yaitu rangkaian seri dan rangkaian paralel. Gambar di atas menunjukkan masing-masing rangkaian resi dan rangkaian paralel.

Gambar a menunjukkan rangkaian seri dari 3 buah resistor. Ketiga resistor dirangkai dengan menyambung ujung-ujung resistor dalam satu jalur yang sama. Karakteristik rangkaian seri resistor adalah:

a. karena ketiga resistor $\left( {{R}_{1}},{{R}_{2}},\text{ dan }{{R}_{3}} \right)$ memiliki jalur yang sama, maka arus yang listrik pada masing-masing resistor juga sama $\left( {{I}_{1}}={{I}_{2}}={{I}_{3}}=I \right)$

b. ujung-ujung resistor memiliki beda potensial (tegangan) yang membagi tegangan total $\left( V \right)$ menjadi masing-masing bernilai ${{V}_{1}},\ {{V}_{2}},\text{ dan }{{V}_{3}}$, sehingga rangkaian seri biasa disebut sebagai rangkaian pembagi tegangan (voltage divider)

c. $V={{V}_{1}}+{{V}_{2}}+{{V}_{3}}$, dengan masing-masing nilai tegangan adalah:
${{V}_{1}}=I\cdot {{R}_{1}}\quad ;\ {{V}_{2}}=I\cdot {{R}_{2}}\quad ;\ {{V}_{3}}=I\cdot {{R}_{3}}$

d. nilai hambatan pengganti resistor seri adalah ${{R}_{s}}={{R}_{1}}+{{R}_{2}}+{{R}_{3}}$.

Sedangkan Gambar b menunjukkan rangkaian paralel dari 3 buah resistor. Ketiga resistor dirangkai dengan menyambung ujung-ujung resistor dalam satu jalur yang berbeda (jalur bercabang). Karakteristik rangkaian paralel resistor adalah:

a. masing-masing ujung percabangan rangkaian paralel memiliki tegangan yang sama $\left( {{V}_{1}}={{V}_{2}}={{V}_{3}}=V \right)$

b. masing-masing jalur resistor membagi jalur arus listrik, sehingga nilai arus total dibagi menjadi 3 jalur tersebut menjadi ${{I}_{1}},\ {{I}_{2}},\text{ dan }{{I}_{3}}$

c. $I={{I}_{1}}+{{I}_{2}}+{{I}_{3}}$, dengan masing-masing nilai kuat arus listrik adalah:
${{I}_{1}}=\frac{V}{{{R}_{1}}}\quad ;\ {{I}_{2}}=\frac{V}{{{R}_{2}}}\quad ;\ {{I}_{3}}=\frac{V}{{{R}_{3}}}$

d. nilai hambatan pengganti resistor paralel adalah $\frac{1}{{{R}_{p}}}=\frac{1}{{{R}_{1}}}+\frac{1}{{{R}_{2}}}+\frac{1}{{{R}_{3}}}$

Contoh Soal Rangkaian Resistor (Rangkaian Seri Paralel)

(1). Tentukan nilai hambatan pengganti antara titik a dan c dari rangkaian resistor pada gambar di bawah!

Jawab:

Cara mengerjakan soal rangkaian di atas adalah dengan mengategorikan kombinasi rangkaiannya.
Resistor $8\Omega $ terhubung seri dengan $2\Omega $, kemudian kita tentukan hambatan pengganti serinya dulu:

${{R}_{s}}=8+4=12\ \Omega $

Resistor $6\Omega $ terhubung paralel dengan $3\Omega $, dengan nilai hambatan pengganti paralel adalah:

$\begin{align} & \frac{1}{{{R}_{p}}}=\frac{1}{6}+\frac{1}{3} \\ & \frac{1}{{{R}_{p}}}=\frac{1+2}{6}=\frac{3}{6} \\ & {{R}_{p}}=\frac{6}{3}=2\ \Omega \\ \end{align}$

Ternyata hambatan pengganti ${{R}_{s}}$ dan ${{R}_{p}}$ terhubung secara seri, sehingga nilai hambatan pengganti total antara titik a dan c adalah:

$\begin{align} & {{R}_{ac}}={{R}_{s}}+{{R}_{p}} \\ & {{R}_{ac}}=12+2=14\ \Omega \\ \end{align}$

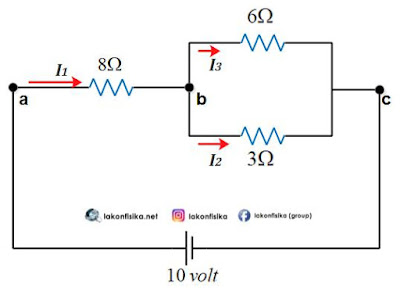
(2). Tentukan nilai masing-masing arus listrik yang mengalir pada rangkaian di bawah ini!

Jawab:

Untuk menentukan nilai ${{I}_{1}}$, harus ditentukan dulu nilai hambatan pengganti total, karena ${{I}_{1}}$ merupakan arus listrik di jalur utama. Cara menentukan hambatan pengganti total seperti contoh nomor 1 di atas.

Hambatan antara titik b dan c adalah paralel, maka:

$\begin{align} & \frac{1}{{{R}_{p}}}=\frac{1}{6}+\frac{1}{3} \\ & \frac{1}{{{R}_{p}}}=\frac{1+2}{6} \\ & {{R}_{p}}=\frac{6}{3}=2\ \Omega \\ \end{align}$

Selanjutnya hambatan pengganti total adalah susunan seri antara hambatan $8\Omega $ dan ${{R}_{p}}$.

${{R}_{T}}=8+2=10\ \Omega $

Nilai ${{I}_{1}}$ adalah: ${{I}_{1}}=\frac{V}{{{R}_{T}}}=\frac{10}{10}=1\ Ampere$

Selanjutnya untuk menentukan nilai ${{I}_{2}}$ dan ${{I}_{3}}$ harus ditentukan nilai ${{V}_{p}}$ terlebih dulu.

$\begin{align} & {{V}_{p}}={{I}_{1}}\cdot {{R}_{p}} \\ & {{V}_{p}}=1\cdot 2=2\ volt \\ \end{align}$

Selanjutnya baru ditentukan nilai ${{I}_{2}}$ dan ${{I}_{3}}$.

$\begin{align} & {{I}_{2}}=\frac{{{V}_{p}}}{3}=\frac{2}{3}\ Ampere \\ & {{I}_{3}}=\frac{{{V}_{p}}}{6}=\frac{2}{6}=\frac{1}{3}\ Ampere \\ \end{align}$

Video Contoh Soal Rangkaian Resistor

Share this post